2.7 Example 6

This example discusses an instance of the limit style of filter design. In previous examples, we specified constraints on the frequency response that were impossible to satisfy. gmeteor's goal was to find the feasible frequency response with the smallest deviation from the constraints. In this example, we change our approach: we specify constraints that can be satisfied, and let gmeteor find a frequency response that satisfies the constraints.

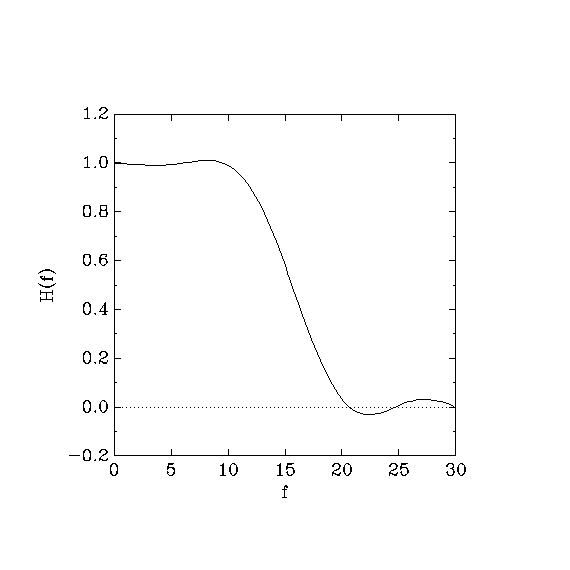
We design a low-pass filter with the following properties: 0.99 <= H(f) <= 1.01 in the passband [0..10], and |H(f)| <= 0.1 in the stopband [20..30]. The stopband ripple must be as small as possible, but we let the passband ripple touch the constraints if necessary. These goals are accomplished by the following specification file.

     ;; Constraint-based filter design.
     
     (title "A simple filter VI")
     (verbose #t)
     (cosine-symmetry)
     (filter-length 10)
     (sampling-frequency 60)
     
     ;; the passband response is constrained within [0.99, 1.01], and it
     ;; is allowed to touch the constraints because the weight is 0.
     (limit-<= (band 0 10) 1.01 0)
     (limit->= (band 0 10) 0.99 0)
     
     ;; the stop response is constrained within [-0.1, 0.1], and it
     ;; is pushed away from the constraints as far as possible, because
     ;; the weight (1) is nonzero.
     (limit-<= (band 20 30) 0.1)
     (limit->= (band 20 30) -0.1)
     
     (output-file "example-6.coef")
     (plot-file "example-6.plot")
     (go)

A graph of the frequency response follows.

The expression (limit-<= band value) specifies that the frequency response should be at most value in the band band. Similarly, the expression (limit-> band value) establishes a lower bound.

How does gmeteor react to this specification file? Recall, from the discussion about weights in Example 2, that gmeteor converts the specifications into the four inequalities H([0..10]) <= 1.01, H([0..10]) >= 0.99, H([20..30]) + y <= 0.1, and H([20..30]) - y >= -0.1. (The weight is zero for the first two inequalities, and therefore the deviation parameter y does not appear in them.) Recall also that gmeteor designs H(f) so as to maximize the deviation parameter y. In our case, y can be interpreted as “distance from the stopband bounds,” and its maximum value is y=0.069 (as shown in the output file). Because the passband weights are 0, gmeteor does not attempt to push H(f) away from the bounds in the passband, and the passband ripple amplitude turns out to be exactly 0.01.

This style of constraint-based filter design is the one described in the METEOR paper. In fact, METEOR does not allow equality constraints, nor does it allow negative values of y. I find the approximation style easier in many cases, because it requires only one constraint instead of a pair of upper and lower bounds. On the other hand, the limit approach is more powerful, as shown in the METEOR paper. Consequently, gmeteor supports both styles, and you can choose the design approach that best suits your problem.