The goal of this example is to teach you some basics of the Scheme
programming language, because gmeteor will be much more useful to
you once you know Scheme. To learn Scheme, I recommend the book
Structure and Interpretation of Computer Programs, by Hal Abelson
and Gerry Sussman—probably the best Computer Science book ever
written.
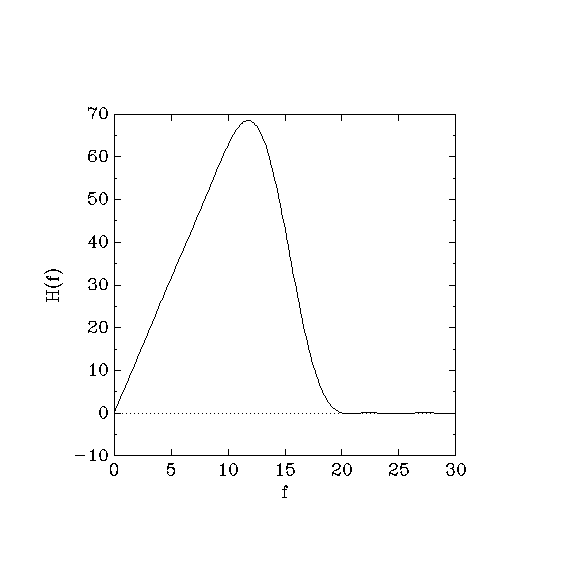
In this example, we want to design a partial-band differentiator,
which is a filter with sine symmetry whose frequency response
H(f) is proportional to the frequency f in the band
[0..10] of interest. In previous examples, the frequency response
was constant within this band, but now we want to specify a nonconstant
frequency response. To this extent, the bound in limit-= will be
a function rather than a number. The following specification
file implements the design.
(title "A simple filter IV")
(verbose #t)
(sine-symmetry)
(filter-length 10)
(sampling-frequency 60)
(define 2pi (* 8 (atan 1)))
(limit-= (band 0 10) (lambda (f) (* 2pi f)))
(limit-= (band 20 30) (lambda (f) 0))
(output-file "example-4.coef")
(plot-file "example-4.plot")
(go)
A graph of the frequency response follows.

The “passband” [0..10] is specified by the expression
(limit-= (band 0 10) (lambda (f) (* 2pi f)))
This expression states that the frequency response must be equal to
2 PI f in the band [0..10]. (In previous examples, we
used the constant value 1.) lambda is the magic Scheme
keyword that creates functions. In Scheme, the syntax (lambda
(var) body) produces a function of the variable var
that, when applied to an argument, evaluates body after binding
the variable var to the argument. In our case, the variable is
f, and the body (* 2pi f).
Once you have a function, how do you apply it? If fun is a
function and expr is any expression, the syntax (fun
expr) denotes the application of fun to the value of
expr. Functions in Scheme are not restricted to only one
argument. For example, sine-symmetry is a function of zero
arguments, and limit-= is a function of two arguments. Indeed,
all expressions that we called commands in Example 1 are
function applications.
You can now play with gmeteor and build your own frequency responses.
To this extent, you need to know that +, -, *, and
/ are functions of two arguments, so that (+ 1 2)
evaluates to 3. For example, you can build a filter with
response (lambda (f) (* (* 2pi f) (* 2pi f))) (a double
differentiator). Scheme provides many other primitive functions that
you can use, e.g., sin, cos, log, and exp.
For a complete list of all Scheme primitives, see the paper
Revised^5 Report on the Algorithmic Language Scheme, by Richard
Kelsey, William Clinger, and Jonathan Rees, editors.